확률적 식별 모델 Probabilistic Descriminative Models
사후확률을 x에 관한 함수로 파라미터화 시키고, MLE를 통해 파라미터를 구한다.
입력벡터 x 대신 비선형 기저함수를 사용한다.
클래스 C1의 사후확률은 특성벡터의 선형함수가 로지스틱 시그모이드를 통과하는 함수이다
파이가 입력이다
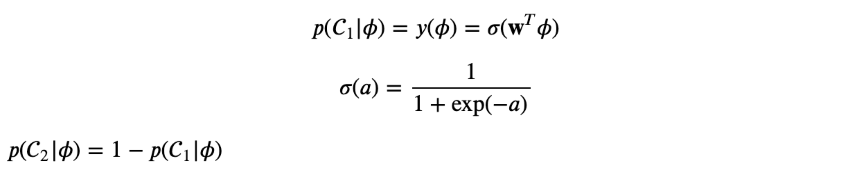
특성벡터가 M 차원이라면 구해야 할 파라미터의 개수는 M개이다
생성모델에서 M(M+5)/2+1 개의 파라미터를 구해야 한다
최대우도해

우도함수
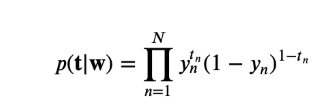
음의 로그우도 The Negative Logarithm of the Likelihood
음의 우도함수를 최소화하는 방식으로 풀 수 있다.
p 목표값

이것을 크로스 엔트로피 에러함수 Cross Entropy Error Function

이산확률변수의 경우

일반적으로 Cross Entropy 가 최소화 될때 두 확률분포의 차이가 최소화 된다.
에러함수 E(W)를 최소화시키는 것을 두가지 관점으로 보면
- 우도를 최대화 시키는 것
- 모델의 예측값의 분포와 목표변수의 분포의 차이를 최소화 하는 것
분포문제에서는 최소제곱법이 아닌 크로스 엔트로피를 사용해야 한다.
회귀문제에서는 최소제곱법을 사용해야 한다.
에러함수 w에 대한 gradient를 구한다.
전체 에러값에서 w를 구해야 하기 때문에 미분한다.


다중클래스 로지스틱 회귀 Multiclass Logistic Regression
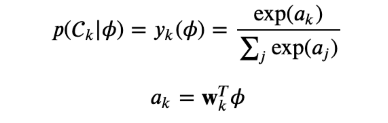
우도함수
특성벡터를 위한 목표벡터 tn은 클래스에 해당하는 하나의 원소만 1이고, 나머지는 0인 1-of-K 인코딩으로 표현된다

Wj에 대한 gradient를 구한다
하나의 샘플에 대한 에러


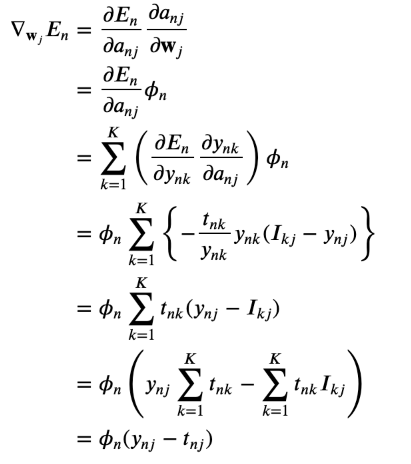
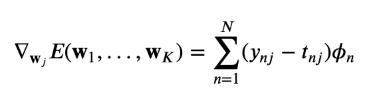
'인공지능 AI > ML' 카테고리의 다른 글
| 보스턴 주택가격 ML 사이킷 런 sklearn 앙상블 Hyper parameter 튜닝 (0) | 2022.10.22 |
|---|---|
| 전이학습 Transfer Learning (0) | 2022.03.27 |
| 선형분류 Linear Models for Classification 확률적 생성 모델 (0) | 2022.01.26 |
| 선형분류 Linear Models for Classification 결정이론 최소제곱법 퍼셉트론 SGD (0) | 2022.01.26 |
| 선형 회귀 Linear Models for Regression 최소제곱법 베이지안 편향분산분해 (0) | 2022.01.25 |












































































































































