분류의 목표
입력벡터 x를 K 개의 가능한 클래스 중에 하나의 클래스에 할당하는 것
분류를 위한 결정이론
확률적 모델 Probabilistic Model
- 생성모델 Generative Model : 사전확률과 확률을 모델링 한 후, 베이즈 정리를 통해 사후확률을 구한다.
또는 결합확률을 직접 모델링 할 수도 있다.
- 식별모델 Discriminative : 사후확률을 직접 모델링
판별함수 Discriminant Function
- 입력 x를 클래스로 할당하는 판별함수를 찾는다
- 확률값을 계산하지 않는다
입력 X를 클래스로 할당하는 판별함수를 찾을 때, 함수가 선형함수라면 선형 판별함수는 다음과 같다.
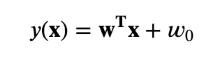
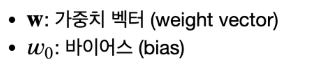
선형판별함수 y(x) 가 0보다 크거나 같을 경우 C1, 0보다 작은 경우 C2로 판별한다.
결정경계 Decision Boundary 는 다음과 같다.

그림으로 그래프를 표현하면

결정 경계면 위의 두 점 Xa와 Xb 는

빨간선은 결정경계면이고, w벡터가 결정경계면에 직교한다.
원점에서 빨간 선까지 거리에 미치지 못하는 것은 C2, 빨간 선을 넘는 것을 C1이라고 한다.
벡터 w를 원점에서 결정경계면에 대한 사영이라고 할 때.

w0은 결정 경계면의 위치를 결정한다.
- w0 < 0 이면 결정 경계면은 원점으로부터 w가 향하는 방향으로 멀어져 있다
- w0 > 0 이면 결정 경계면은 원점으로부터 w의 반대방향으로 멀어져 있다
이때 y(x) 값은 x와 결정경계면 사이의 부호화된 거리와 비례한다.
임의의 한 점 x의 결정 경계면에 대한 사영에서 다음의 식이 나온다.
여기서 r은 x가 결정경계면으로 직교하는 선을 사영했을 때 그 거리를 의미한다.
그래프에서 파란 점선으로 확인할 수 있다.

- y(x) > 0 이면 x는 결정 경계면을 기준으로 w가 향하는 방향에 있다
- y(x) < 0 이면 x는 결정 경계면을 기준으로 -w가 향하는 방향에 있다
- y(x)의 절대값이 클 수록 더 멀리 떨어져 있다
가짜 입력 Dummy Input x0 = 1을 이용해서 수식을 단순화 시키면
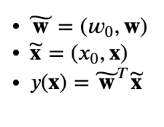
분류를 위한 최소제곱법 Least Squares for Classification
결정경계면에 닿았는지를 판별하는 C1, C2 값들을 실수로 만들면 최소제곱법을 사용할 수 있다.

위와 같은 판별함수에서

제곱합 에러함수





판별함수는 다음과 같다.

최소 제곱법의 단점은 다음과 같다
- 극단치, 이상치 Outlier에 민감
- 목표값의 확률분포에 대한 잘못된 가정에 기초
보라색선이 최소제곱법
녹색선은 로지스틱 regression

퍼셉트론 알고리즘 The Perceptron Algorithm

f는 활성함수 Activtion Function으로 퍼셉트로는 다음의 계단형 함수를 사용한다.



목표값이 옳다면 0보다 큰 양수값을 가져야 한다.
에러가 생긴다면 Ep(w) 값이 음수 값을 가질 것이다.

에러함수가 주어지면 SGD를 통해 결정경계면을 알아낼 수 있다.

잘못 분류된 샘플에는 다음과 같은 영향을 준다.

마지막 그림이 이상적인 분류 그림이고 나머지는 점진적으로 분류가 진행되는 모습이다.
두 가지 모델은 지금은 쓰이지 않는다.
분류 모델의 기초가 되었지만 현재는 더 정확한 알고리즘이 나왔기 때문이다.
'인공지능 AI > ML' 카테고리의 다른 글
| 선형분류 Linear Models for Classification 확률적 식별 모델 (0) | 2022.01.27 |
|---|---|
| 선형분류 Linear Models for Classification 확률적 생성 모델 (0) | 2022.01.26 |
| 선형 회귀 Linear Models for Regression 최소제곱법 베이지안 편향분산분해 (0) | 2022.01.25 |
| 선형회귀 모델 Linear Models for Regression 다항식 시그모이드 SGD Normal Equations (0) | 2022.01.24 |
| 확률 변수 Probability Distributions ml (0) | 2022.01.20 |
